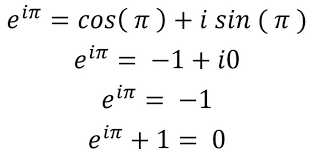교과과정에서 배우는 수학에서도 계산 과정과 방법만 배우는 것이 아니라 탄생의 배경이라든가 현실 세계에서 어떻게 활용되는지.. 그런 맥락 속에서 배우기 바란다.
아이에게 그런 부분을 조금이라도 채워주고 싶어서 관련 책을 찾아보게 된 수학잡지.
‘Newton HIGHLIGHT 93 실제 사례로 기초부터 응용까지!과학을 발전시킨 수학의 세계지수, 대수, 벡터.
아래 사진과 같다.

일단
‘지수’를 보면
지수의 효용은 큰 수나 작은 수를 간결하게 나타낼 수 있다는 점이다.우주 크기 8800000000000000000000000000000000000000m는 8.8×10의 26제곱 수소 원자의 원자핵 크기는 약 0.0000000000000000001인데 이는 1.0×10의-15제곱으로 간결하게 표현할 수 있다.
다음으로 ‘로그’에 관해서는
대학 공개 강의 사이트인 K-MOOC에서 볼 수 있는 광운대 허민 교수의 <수학사> 강의에 따르면
인류의 5가지 계산 툴로,
- 주판(abacus):주판, 주판을 포함한 개념 2. 인도-아라비아수 체계(Indo-Arabic Numeral System) 3. 소수(decimal) 4. 로그(logarithm) 5. 컴퓨터(the computer)가 있다.
- 특히, 로그 계산 도구로서의 편리성에 대해

라플라스(Pierre-Simon Lapl ace)는
로그 발견은 작업량을 줄임으로써 천문학자의 수명을 두 배로 만들었다고 할 만큼 로그는 천문학의 필요에 의해 탄생했고 천문학 발전에 크게 기여한 것 같다.
“로그가 고안된 것은 1594년. 당시는 서영의 이른바 ‘대항해시대’로 해상에서 배의 위치 측량처럼 큰 수를 계산하는 경우가 많아졌다.또한 행성에 대한 상세한 관찰이 이루어지고 천동설에서 지동설로 바뀐 시대에서 행성의 궤도 계산 등에서도 복잡한 계산이 필요. 조금이라도 계산하기 쉽게 하자는 시대적 요청이 나온 시기였다.
이러한 상황에서 영국의 네이피아가 고안한 로그는 현대의 정의와는 다르지만 본질적으로 같은 것이었다.곱셈과 나눗셈을 각각 덧셈과 뺄셈으로 바꿀 수 있다.

존 네이피아(John Napie r, 1550-1617)
*스코틀랜드 마치스톤의 8대 남작 발명가, SF 소설가*정치인으로 종교적 분쟁, 다툼에 관여* <놀라운 로그 규범 설명?(1614): 로그 개발에 20년 이상 힘을 쏟는다.
존 네이피아의 로그는 즉각 환영을 받았고 브리그스(Henry Briggs, 1561-1631)가 1615년 네이피아를 방문해 상용 로그를 제안하였다. 이 때문에 상용 로그는 브리그스로도 불린다.로그는 천문학 로그를 이용해 곱셈을 덧셈으로 간단하게 계산할 때 활용.
로그는 로그자, 상용 로그표 등에 의해 계산량을 현저하게 줄이는 뛰어난 계산 툴로서 이용되고 있지만, 현재는 컴퓨터가 대체하고 있다.
그래도 로그는 현재까지도 중요한 함수로서의 위치는 계속 지키고 있다.대수함수는 미분하면 유리함수가 되는 관계로부터 미분적분학에서 결코 빼놓을 수 없는 함수이다.
또한 대수 척도는 물리적인 양을 매우 쉽게 표현할 수 있기 때문에 다양한 분야에서 사용되고 있다.(음높이, 데시벨dB, 항성등급, 지진 규모, 수소이온 농도, 기압 고도계 등)
또, 로그는 계산 도구를 넘은 존재이며, 로그는 특별한 수인 자연상수 「e」의 존재를 인류에게 알린다.
스위스의 수학자 레옹하르트 오일러(1707-1783)는 ‘로그 함수’를 미분하는 과정에서 ‘e’라는 특별한 수를 발견했다.e를 로그 발견자인 네이피어를 기념해 네이피어 수라고 부르기도 한다.현재 ‘e’는 자연현상, 실험결과, 경제활동 등에서 볼 수 있는 ‘변화’를 수학적으로 분석할 때 매우 중요한 역할을 한다.
또 e의 발견으로 세상에서 가장 아름다운 공식으로 불리며 물리학자 리처드 파인먼이 인류의 보물로 부른 오일러의 공식도 탄생하게 됐다.