2023 수능특강 수학 25. 도함수 활용(2) 문제 해설입니다.
2023 수능특강 수학 25. 도함수 활용(2) 문제 해설입니다.

2023 수능특강 수학 25. 도함수 활용(2) 문제 해설입니다.

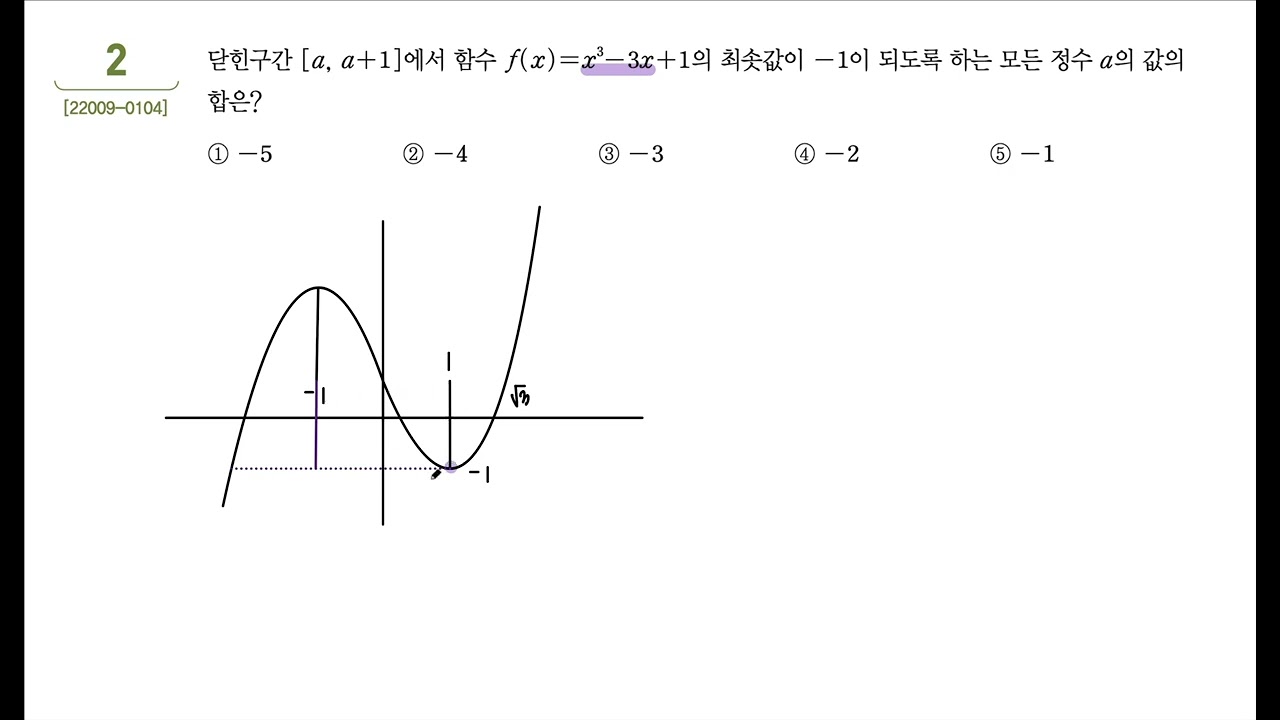
문제1번입니다.최고차항계수가양수인3차함수이기때문에그래프개형을그려놓고미분해서극점을체크해놓겠습니다. 이때 주어진 구간에서 최대값은 f(-1)일 때이고 최소값은 f(-2)와 f(2) 중 더 작은 값이 최소값이 됩니다. 문제 2번입니다. 주어진 식을 미분하여 그래프의 변형을 그리고 극점을 표시합니다.최소값이 -1이 되려면 x = -1일 때의 극소점 또는 x = -2가 되는 점입니다. 따라서 구간을 잘 정리해서 생각해보면 a= =2, 0, 1이 되겠네요.

문제1번입니다.최고차항계수가양수인3차함수이기때문에그래프개형을그려놓고미분해서극점을체크해놓겠습니다. 이때 주어진 구간에서 최대값은 f(-1)일 때이고 최소값은 f(-2)와 f(2) 중 더 작은 값이 최소값이 됩니다. 문제 2번입니다. 주어진 식을 미분하여 그래프의 변형을 그리고 극점을 표시합니다.최소값이 -1이 되려면 x = -1일 때의 극소점 또는 x = -2가 되는 점입니다. 따라서 구간을 잘 정리해서 생각해보면 a= =2, 0, 1이 되겠네요.

문제1번입니다.최고차항계수가양수인3차함수이기때문에그래프개형을그려놓고미분해서극점을체크해놓겠습니다. 이때 주어진 구간에서 최대값은 f(-1)일 때이고 최소값은 f(-2)와 f(2) 중 더 작은 값이 최소값이 됩니다. 문제 2번입니다. 주어진 식을 미분하여 그래프의 변형을 그리고 극점을 표시합니다.최소값이 -1이 되려면 x = -1일 때의 극소점 또는 x = -2가 되는 점입니다. 따라서 구간을 잘 정리해서 생각해보면 a= =2, 0, 1이 되겠네요.

문제 3번입니다. 방정식에서 서로 다른 실근의 개수를 묻는 문제는 ~~=a 이렇게 계수가 +1인 미지수 형태로 놓으라고 했습니다. 8로 나누는데 조금 번거롭지만 나중에 틀리지 않으려면 이렇게 하는 게 좋아요. 이때 왼쪽 변(~~~)의 그래프를 잘 그려서 실근의 개수를 잘 세면 됩니다. 문제 4번입니다. 부등식 문제는 a까지 전부 왼쪽으로 이항해서 풀게요. 이항하고 미분하면 없어지잖아요. 그때 0보다 크려면 극소치가 0보다 크면 모든 함수의 그래프가 0보다 항상 커집니다. 대입해서 a의 값을 구하면 되겠지요.

문제 3번입니다. 방정식에서 서로 다른 실근의 개수를 묻는 문제는 ~~=a 이렇게 계수가 +1인 미지수 형태로 놓으라고 했습니다. 8로 나누는데 조금 번거롭지만 나중에 틀리지 않으려면 이렇게 하는 게 좋아요. 이때 왼쪽 변(~~~)의 그래프를 잘 그려서 실근의 개수를 잘 세면 됩니다. 문제 4번입니다. 부등식 문제는 a까지 전부 왼쪽으로 이항해서 풀게요. 이항하고 미분하면 없어지잖아요. 그때 0보다 크려면 극소치가 0보다 크면 모든 함수의 그래프가 0보다 항상 커집니다. 대입해서 a의 값을 구하면 되겠지요.문제 3번입니다. 방정식에서 서로 다른 실근의 개수를 묻는 문제는 ~~=a 이렇게 계수가 +1인 미지수 형태로 놓으라고 했습니다. 8로 나누는데 조금 번거롭지만 나중에 틀리지 않으려면 이렇게 하는 게 좋아요. 이때 왼쪽 변(~~~)의 그래프를 잘 그려서 실근의 개수를 잘 세면 됩니다. 문제 4번입니다. 부등식 문제는 a까지 전부 왼쪽으로 이항해서 풀게요. 이항하고 미분하면 없어지잖아요. 그때 0보다 크려면 극소치가 0보다 크면 모든 함수의 그래프가 0보다 항상 커집니다. 대입해서 a의 값을 구하면 되겠지요.문제 5번입니다. 속도가 2가 되는 시각은 미분이고, 2가 되는 t의 값을 찾아보세요. 이때 t는 시간이기 때문에 음의 값은 존재하지 않습니다. 가속도는 두 번 미분하면 되겠네요.문제 6번이에요. 사이의 거리가 8이 되는 시각은 두 위치를 빼면 거리가 되지만 거리도 음수는 없어요. 따라서 두 식을 제외하고 절대값을 매겨야 합니다. 그러면 t의 값이 2인 것을 알 수 있고 속도는 미분해서 t에 2를 대입하면 되겠네요.답을구했으니까마무리하셔도되지만절대값풀때-8일때도계산을해보시면t가양일때해당하는값이없는것을알수있습니다.문제 5번입니다. 속도가 2가 되는 시각은 미분이고, 2가 되는 t의 값을 찾아보세요. 이때 t는 시간이기 때문에 음의 값은 존재하지 않습니다. 가속도는 두 번 미분하면 되겠네요.문제 6번이에요. 사이의 거리가 8이 되는 시각은 두 위치를 빼면 거리가 되지만 거리도 음수는 없어요. 따라서 두 식을 제외하고 절대값을 매겨야 합니다. 그러면 t의 값이 2인 것을 알 수 있고 속도는 미분해서 t에 2를 대입하면 되겠네요.답을구했으니까마무리하셔도되지만절대값풀때-8일때도계산을해보시면t가양일때해당하는값이없는것을알수있습니다.문제 5번입니다. 속도가 2가 되는 시각은 미분이고, 2가 되는 t의 값을 찾아보세요. 이때 t는 시간이기 때문에 음의 값은 존재하지 않습니다. 가속도는 두 번 미분하면 되겠네요.문제 6번이에요. 사이의 거리가 8이 되는 시각은 두 위치를 빼면 거리가 되지만 거리도 음수는 없어요. 따라서 두 식을 제외하고 절대값을 매겨야 합니다. 그러면 t의 값이 2인 것을 알 수 있고 속도는 미분해서 t에 2를 대입하면 되겠네요.답을구했으니까마무리하셔도되지만절대값풀때-8일때도계산을해보시면t가양일때해당하는값이없는것을알수있습니다.#22009-0103 #22009-0104 #22009-0105 #22009-0106 #22009-0107 #2023수학능력시험특강해설 #2023수능특강수학2 #2023수능특강해설 #수학2해설 #도함수활용 #유제해설