수학의 사칙연산, 수에 대해서 공부를 하게 되면 가장 먼저 배우는 것이 사칙연산입니다. 덧셈, 뺄셈, 곱셈, 나눗셈의 네 가지 계산이 됩니다. 처음에는 자연수에서 시작해서 나중에는 모든 영역의 수에 대해 배웁니다. 그 중에서 어린 아이들이 조금은 혼란스러워 하는 부분 중의 하나가 분수 계산법을 배우면서 힘들 것 같습니다. 그 이유는 자연수는 하나하나 잘 나눌 수 있습니다 수학의 사칙연산, 수에 대해서 공부를 하게 되면 가장 먼저 배우는 것이 사칙연산입니다. 덧셈, 뺄셈, 곱셈, 나눗셈의 네 가지 계산이 됩니다. 처음에는 자연수에서 시작해서 나중에는 모든 영역의 수에 대해 배웁니다. 그 중에서 어린 아이들이 조금은 혼란스러워 하는 부분 중의 하나가 분수 계산법을 배우면서 힘들 것 같습니다. 그 이유는 자연수는 하나하나 잘 나눌 수 있습니다
예를 들어서 사과를 하나둘씩 머리로 이해하기가 쉽지만 절반이라는 것을 수로 표현하라고 하면 갑자기 어려워지기 시작합니다. 이것을 표현하기 위해 등장한 것이 분수입니다 분모와 분자로 이루어진 수로, 여기서 ‘분’은 ‘나누다’의 한자어로, 분모는 어머니를 나누고 분자는 아들을 나눈 이렇게 따로 보면 의미가 애매하죠? 이 두 가지 의미를 합쳐서 해석하면 다음과 같습니다. 예를 들어서 사과를 하나둘씩 머리로 이해하기가 쉽지만 절반이라는 것을 수로 표현하라고 하면 갑자기 어려워지기 시작합니다. 이것을 표현하기 위해 등장한 것이 분수입니다 분모와 분자로 이루어진 수로, 여기서 ‘분’은 ‘나누다’의 한자어로, 분모는 어머니를 나누고 분자는 아들을 나눈 이렇게 따로 보면 의미가 애매하죠? 이 두 가지 의미를 합쳐서 해석하면 다음과 같습니다.

기준이 되는 전체(어머니)로 나누어진 수(아들)를 말합니다. 예를 들어, 3/5이라는 분수가 있다면 전체 5개 중 3만을 나누었다는 의미가 된다면, 이런 분수는 왜 사용하는 것일까요? 답을먼저말하면나머지가떨어지지않는나눗셈이있기때문입니다. 물론 떨어지는 숫자도 분수로 표현할 수 있지만 분수 표현의 주된 목적은 나눌 때 명확한 답이 나오지 않기 때문에 표현한 수식이 됩니다. 1/2은 0.5라는 숫자가 나오는데 1/3은 0.9999999999…라는 무한소수로 표현되기 때문에 분수식을 사용하면 쉽게 표현할 수 있잖아요~ 기준이 되는 전체(어머니)로 나누어진 수(아들)를 말합니다. 예를 들어, 3/5이라는 분수가 있다면 전체 5개 중 3만을 나누었다는 의미가 된다면, 이런 분수는 왜 사용하는 것일까요? 답을먼저말하면나머지가떨어지지않는나눗셈이있기때문입니다. 물론 떨어지는 숫자도 분수로 표현할 수 있지만 분수 표현의 주된 목적은 나눌 때 명확한 답이 나오지 않기 때문에 표현한 수식이 됩니다. 1/2은 0.5라는 숫자가 나오는데 1/3은 0.9999999999…라는 무한소수로 표현되기 때문에 분수식을 사용하면 쉽게 표현할 수 있잖아요~
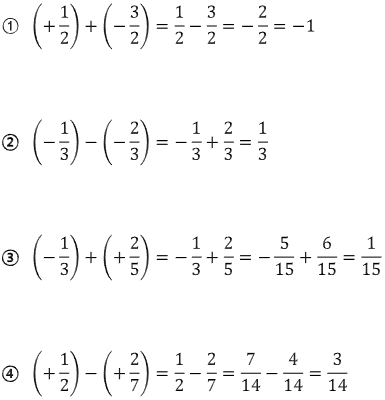
여러 가지 이유가 있지만 아마 분수를 사용하는 이유는 무리수 표현을 하기 위한 하나의 방법이 아닐까 싶습니다. 그러면 새로운 분수 계산법의 사칙연산을 살펴보도록 하겠습니다. 가장 기본이 되는 분수의 덧셈을 해볼까요? 분수의 덧셈에서 가장 중요한 개념은 통분을 한다고 합니다. 통분이란 쉽게 말하면 더하고 싶은 대상과의 눈높이를 맞추는 것입니다. 예를들어계단에두친구가각각다른위치에있다고가정하면 여러 가지 이유가 있지만 아마 분수를 사용하는 이유는 무리수 표현을 하기 위한 하나의 방법이 아닐까 싶습니다. 그러면 새로운 분수 계산법의 사칙연산을 살펴보도록 하겠습니다. 가장 기본이 되는 분수의 덧셈을 해볼까요? 분수의 덧셈에서 가장 중요한 개념은 통분을 한다고 합니다. 통분이란 쉽게 말하면 더하고 싶은 대상과의 눈높이를 맞추는 것입니다. 예를들어계단에두친구가각각다른위치에있다고가정하면

함께 같은 자리에 앉기 위해서는 두 가지 방법이 있는데, 둘 중 한 명의 친구가 상대방에게 다가가거나 혹은 두 명의 친구가 특정 위치에서 만나자고 하는 경우가 됩니다. 이 두 경우 모두를 통분으로 같은 장소를 만들어주는 역할을 하는 것입니다. 예를 통해서 보면 쉽게 이해할 수 있습니다. 함께 같은 자리에 앉기 위해서는 두 가지 방법이 있는데, 둘 중 한 명의 친구가 상대방에게 다가가거나 혹은 두 명의 친구가 특정 위치에서 만나자고 하는 경우가 됩니다. 이 두 경우 모두를 통분으로 같은 장소를 만들어주는 역할을 하는 것입니다. 예를 통해서 보면 쉽게 이해할 수 있습니다.

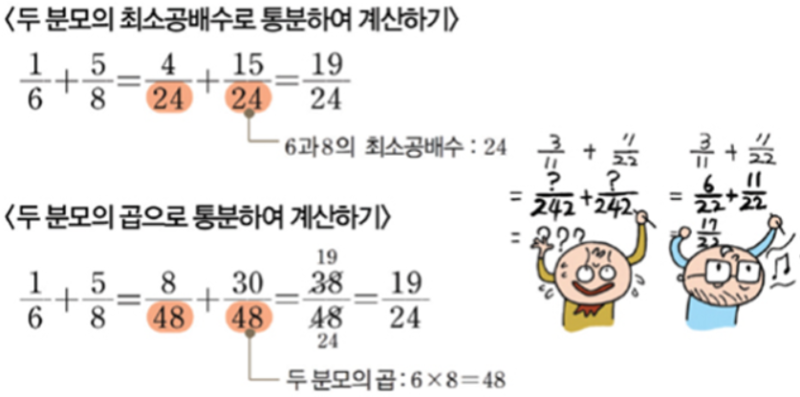
이렇게 분모가 2와 4의 두 분수의 덧셈을 구할 때 앞서 말한 계단을 생각해 보면 첫 번째 한 친구가 4층에 있는 친구를 위해 올라가거나 아래에 있는 2층 친구를 가거나 아니면 둘 다 8층에서 만나는 경우가 있습니다. 이렇게분모를같은층으로만드는작업을통분이라고합니다. 통가루와 함께 나오는 개념이 최소공배수인데요~ 2개 이상의 수를 최소한의 수를 곱하여 최종적으로 아래의 수를 같게 만드는 것입니다~ 위의 예를 다시 들자면, 2와 4의 최소공배수는 4가 되기 때문에 세 가지 경우 중 4층에서 만나는 것이 가장 효율적이라고 할 수 있습니다~ 분수의 덧셈을 곱셈처럼 간단하게 하는 방법, 분수의 덧셈을 분수의 곱셈과 같이 하는 계산법이 있는데, 잘 생각해보면 쉽습니다. 이렇게 분모가 2와 4의 두 분수의 덧셈을 구할 때 앞서 말한 계단을 생각해 보면 첫 번째 한 친구가 4층에 있는 친구를 위해 올라가거나 아래에 있는 2층 친구를 가거나 아니면 둘 다 8층에서 만나는 경우가 있습니다. 이렇게분모를같은층으로만드는작업을통분이라고합니다. 통가루와 함께 나오는 개념이 최소공배수인데요~ 2개 이상의 수를 최소한의 수를 곱하여 최종적으로 아래의 수를 같게 만드는 것입니다~ 위의 예를 다시 들자면, 2와 4의 최소공배수는 4가 되기 때문에 세 가지 경우 중 4층에서 만나는 것이 가장 효율적이라고 할 수 있습니다~ 분수의 덧셈을 곱셈처럼 간단하게 하는 방법, 분수의 덧셈을 분수의 곱셈과 같이 하는 계산법이 있는데, 잘 생각해보면 쉽습니다.
먼저 두 수의 분모를 곱해서 씁니다. 예는 3 곱하기 5이므로 15가 됩니다. 그리고 서로 크로스로 분수 곱하기를 합니다. 그러면 6과 5가 나옵니다. 이 두 가지를 더하는 것만으로 끝! 만약 약간의 의심이 있다면 일단 어떤 분수식도 똑같이 계산해보면 최종 정답은 같다는 사실! 어떻게 보면 당연할 수도 있지만 저렇게 그림을 그리고 풀면 실수를 줄일 수 있어요~ 분수 곱셈처럼 보이는 덧셈 계산법 아닐까요? 이상으로 분수플러스를 조금 편하게 계산해보자는 일종의 트릭에 대해 알아봤습니다~ 먼저 두 수의 분모를 곱해서 씁니다. 예는 3 곱하기 5이므로 15가 됩니다. 그리고 서로 크로스로 분수 곱하기를 합니다. 그러면 6과 5가 나옵니다. 이 두 가지를 더하는 것만으로 끝! 만약 약간의 의심이 있다면 일단 어떤 분수식도 똑같이 계산해보면 최종 정답은 같다는 사실! 어떻게 보면 당연할 수도 있지만 저렇게 그림을 그리고 풀면 실수를 줄일 수 있어요~ 분수 곱셈처럼 보이는 덧셈 계산법 아닐까요? 이상으로 분수플러스를 조금 편하게 계산해보자는 일종의 트릭에 대해 알아봤습니다~